现代优化算法-启发式介绍+禁忌算法+模拟退火

顾问全程陪同指导让您无忧

免费看墓专车上门接送

购墓优惠折扣多还有赠品

殡葬一条龙让您省心省事

大家都在关注: 前端性能优化知识梳理; 抖音下载过的软件记录怎么查询; 拓扑结构图; 从短视频到直播，再到全域兴趣电商，2023抖音增长趋势是什么？; Steam实验室上线玩家DLC中心看看自己“省”了多少钱; 政已阅丨攻坚营商环境优化提升浙江再寻“路”; 我想要出国留学学室内设计，那个国家比较好，。费用也相对低些。最好是说英语的国家，麻烦详细些？; 2023抖音趋势赛道风向标（食品饮料行业专刊）

现代优化算法-启发式介绍+禁忌算法+模拟退火

2024-04-15 12:38 作者：佚名

由于之前用公众号，第一次来知乎，所有一下发所有库存哈~

之后会学一个算法，发一下~~

自己也是初学者，可能有错，一起学习啦~~

1. 启发式算法

2. 禁忌算法（Tabu Search）

3. 模拟退火算法

在某些情况下，特别是实际问题中，最优算法的计算时间使人无法忍受或因问题的难度使其计算时间随实例规模的增加以指数速度增加，如表1.2.1列举的TSP枚举算法的情况，此时只能通过启发式算法求到实例的一个可行解。

启发式算法是一种技术。这种技术使得在可接受的计算费用内去寻找最好的解，但不一定能保证所得解的可行性和最优性，甚至在多数情况下，无法阐述所得解同最优解的近似程度。

采用最坏实例下的误差界限来评价启发式算法，则可以定义近似算法：

称H是A的 ε 近似算法当且仅当：

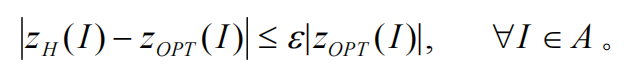
现代优化算法是20世纪80年代初以来得到深入研究和广泛应用的启发式算法。主要包括贪婪算法(greedy algorithm)、邻域搜索(local search)算法、禁忌搜索算法，模拟退火算法，遗传算法，蚁群优化算法，人工神经网络算法等。

相比于最优化算法，启发式算法能够迅速发展的优点：

数学模型本身是实际问题的简化，或多或少地忽略了一些因素；而且数据采集具有不精确性；参数估计具有不准确性；这些因素可能造成最优算法所得到的解比启发式算法所得到的解更差。
有些难的组合最优化问题可能还没有找到最优算法（例如NP-Hard问题），即使存在，由算法复杂性理论，它们的计算时间是无法接受或不实际的。
一些启发式算法可以用在最优算法中。如在分枝定界算法中，可以用启发式算法估计下（上）界。

局部领域搜索算法的推广

在使用局部搜索算法时，邻域结构和初始点的选取非常关键

人工智能在组合优化问题中的一个成功应用

领域搜索+禁忌表

为了找到“全局最优解”，就不应该执着于某一个特定的区域。局部搜索的缺点就是太贪婪地对某一个局部区域以及其邻域搜索，导致一叶障目，不见泰山。禁忌搜索就是对于找到的一部分局部最优解，有意识地避开它（但不是完全隔绝），从而获得更多的搜索区间。兔子们找到了泰山，它们之中的一只就会留守在这里，其他的再去别的地方寻找。就这样，一大圈后，把找到的几个山峰一比较，珠穆朗玛峰脱颖而出。

当兔子们再寻找的时候，一般地会有意识地避开泰山，因为他们知道，这里已经找过，并且有一只兔子在那里看着了。这就是禁忌搜索中禁忌表（tabu list) 的含义。那只留在泰山的兔子一般不会就安家在那里了，它会在一定时间后重新回到找最高峰的大军，因为这个时候已经有了许多新的消息，泰山毕竟也有一个不错的高度，需要重新考虑，这个归队时间，在禁忌搜索里面叫做禁忌长度（tabu length）；如果在搜索的过程中，留守泰山的兔子还没有归队，但是找到的地方全是华北平原等比较低的地方，兔子们就不得不再次考虑选中泰山，也就是说，当一个有兔子留守的地方优越性太突出，超过了“best so far”的状态，就可以不顾及有没有兔子留守，都把这个地方考虑进来，这就叫特赦准则（aspiration criterion）。这三个概念是禁忌搜索和一般搜索准则最不同的地方，算法的优化也关键在这里。

禁忌长度：

过短：在一个局部最优解内循环
过长：造成算法的领域点都为T标记，被禁，无法进行

其中 $STEP 2$ 不受禁忌的元素包含两类：一类是那些没有被禁忌的元素，另一类是可以被解除禁忌的元素。

组成元素

造成解变化的状态为禁忌对象。

解的变化

解的分量的变化

目标值变化

初始点为 $x$ ，目标值值为 $a$ , $H(a)=\\left\\{ x\\in D | f(x)=a \\right\\}$ 。
两个目标值蕴含着两个解集。

相对来说，1，2，3三种方法的禁忌范围逐渐变大，计算快，但是搜索范围表小，易陷入局部最优解。

禁忌对象被禁用的次数，也可以用禁忌集合T长度去更新被禁对象。

出现候选集中的全部对象都被禁忌

或一对象被禁但若解禁后其当前最优值将下降的情况。

如果一个影响大的变化成为被禁对象，我们应该使其自由

一般思想，具体问题具体分析！

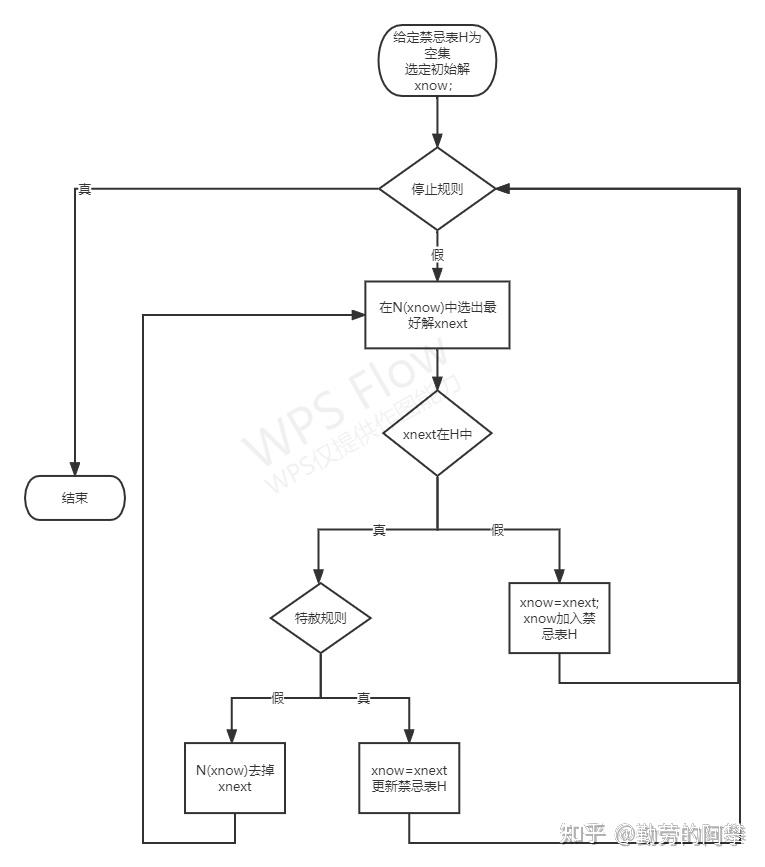
禁忌算法：处理TSP问题的python代码[1]

实测可以跑通
其中设定了一个长度为10的禁忌表，运用确定步数终止，但需要记录最优解。

扩展局部搜索算法的方面：以一定概率选择领域中费用值大的状态，跳出局部最优解
一种升温再降温回原温度的方法，从而达到最小内能稳定
金属达到稳定状态，就相当于最优化问题找到最优解

右统计力学表示，温度T时。分子在状态r的概率分布满足波兹曼(Boltzmann)函数:

$Pr \\left\\{\\bar E=E(r)\\right\\}=\\frac{1}{Z(T)}exp(-\\frac{E(r)}{k_BT}) \\\\$

其中， $\\bar E$ 为一个随机变量， $E(r)$ 为在温度T下处以状态r的能量， $Z(T)$ 为概率分布的标准化因子 $Z(T)=\\sum_{s\\in D}exp\\left\\{ -\\frac{E(s)}{k_BT}\\right\\}$ ， $k_B>0$ 为波兹曼常数。

1.由公式可知，当温度很高时，概率分布接近平均分布

2.由求导可知，固定最小能量状态为 $r_{min}$ ，则 $Pr \\left\\{\\bar E=E(r)\\right\\}$ 关于温度T时单调下降的。

3.当T趋于0时， $Pr \\left\\{ \\bar E=E(r_{min})\\right\\}\\rightarrow \\frac{1}{|D_0|}$ ,其中 $D_0$ 为具有最低能量的所有状态集合。表明模拟退火方法以接近概率1的可能逼近最优解

将组合优化问题同金属物体退火进行类比：

算法：

流程图：

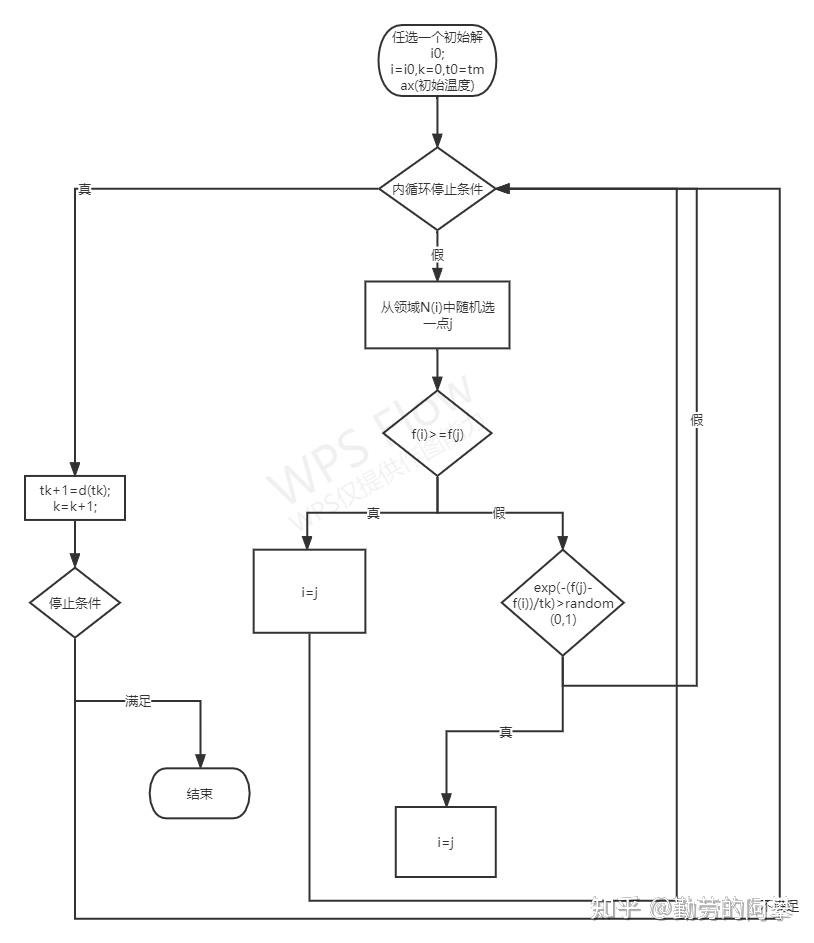
学到现在，感觉跟禁忌算法差不多，都是给非局部最小解一个可能。禁忌约束局部最优解，模拟退火给一概率选非最优解。

利用马尔可夫链进行建立。

由于给定领域结构后，模拟退火过程是一个状态转移到另一个状态不断的随机游走。状态i转移到状态j的概率为：

$\\begin{equation*}p_{ij}(t)=\\end{equation*}\\begin{cases}G_{ij}(t)A_{ij}(t)，&\\forall j\ eq i，\\\\ 1-\\sum_{l=1,l\ eq i}^{|D|}G_{il}(t)A_{il}(t)， &j=i；\\end{cases}\\\\$

其中 $G_{ij}(t)$ 表示在状态i，状态j被选取的概率,假设领域中元素等概率选取时：

$\\begin{equation*}G_{ij}(t)=\\end{equation*}\\begin{cases}\\frac{1}{|N(i)|},&j\\in N(i)，\\\\ 0，&j\ otin N(i)；\\end{cases}\\\\$

$A_{ij}(t)$ 表示产生状态j后，状态j被接受的概率,如在模拟退火算法中接受的概率为

$\\begin{equation*}A_{ij}(t)=\\end{equation*}\\begin{cases}1,&f(i)\\geq f(j)，\\\\ \\exp(-\\frac{\\Delta f_{ij}}{t})，&f(i)< f(j)；\\end{cases}\\\\$

$|D|$ 表示状态集合（解集合）中状态的个数。 $P(t)=(p_{ij}(t))_{|D|\ imes |D|},G(t)=(G_{ij}(t))_{|D|\ imes |D|}\\mbox{和}A(t)=(A_{ij}(t))_{|D|\ imes |D|}$ 分别称为一步转移概率矩阵，产生矩阵和接受矩阵。

上面三个公式为模拟退火的基本数学模型。模拟退火可以分两类：

1.时齐算法：对每一个固定温度，计算一个马尔可夫链，直到达到稳定状态，再让温度下降。
2.非时齐算法：由一个马尔科夫链组成，要求两个相邻的转移中，温度t时下降的。？？

马尔科夫链应满足下列条件：

可达性：无论起点，任何一个状态都可以达到。
渐近不依赖起点
分布稳定性：1.温度不变时，马尔科夫链的极限分布存在。2.当温度渐近0时，马尔科夫链也有极限分布。
收敛到最优解：当温度渐近0时，最优状态的极限分布和为1。

$p_{ij}(n-1)=P(X(n)=j|X(n-1)=i)\\\\$ 为一步转移概率。当状态空间有限时，称为有限马氏链，一步转移概率矩阵记为 $P(n-1)=(p_{ij}(n-1))_{|D|\ imes|D|}\\\\$

当每一步的转移概率矩阵都相等时，称马氏链为时齐的（homogenneous）。

$p_{ij}^{(n)}=P(X(n)=j|X(0)=i) \\\\$

表示n步转移概率。

由此可知，模拟退火的一步转移概率与第几次迭代无关，因此，马氏链是时齐的。

定义从i到达j首达时刻的随机变量为

$T_{ij}=min\\left\\{n|X(0)=i,X(n)=j,n\\geq 1\\right\\}\\\\$

其概率定义为

$f_{ij}^{(n)}=P(T_{ij}=n|X(0)=i) \\\\$

迟早到达概率为

$f_{ij}=\\sum_{n=1}^{\\infty}f_{ij}^{(n)}。 \\\\$

由马氏链性质的讨论，当下面性质得以证明后，说明模拟退火算法收敛全局最优解。

定理 3.3.3 和定理 3.3.4 给出时齐算法全局收敛应满足的充分条件，但这些条件的限制是比较强的，如(3.1.6)的发生概率就不一定满足定理 3.3.3 的(2)，因此，研究模拟退火算法全局收敛应满足的充分条件是理论研究的一个方向。

不能保证解的领域结构中都是可行解：利用罚函数法或构造比较精巧的邻域结构，这样可以节省大量的计算时间
选取初始温度：选取初始温度 $t_{0}$ 使得每一个状态的概率接近相等，即 $exp(-\\frac{\\Delta f_{ij}}{t_0})\ hickapprox 1\\\\$ 故取 $t_0=K\\Delta_0,\\mbox{K充分大的数}\\\\$ 其中 $\\Delta_0=max\\left\\{f(i)|i\\in D\\right\\}-min\\left\\{f(i)|i\\in D\\right\\}$

产生数值计算估计和统计推断估计方法给出一个近似估计值。

3.温度下降方法：固定下降速率或者固定间隔。

4.实际计算中达到理论的平稳分布是不可能的，只能在同一温度时，近似找个步数停止，当作极限。 每一固定温度的迭代长度：固定长度或者由接受和拒绝的比率控制迭代步数。（温度高时，接受的概率大，迭代步数小，温度低，则迭代步数高。）

5.算法的终止原则：零度法、循环总数控制、不改进规则、接受概率控制、领域法...

模拟退火：处理TSP问题的python代码[2]

实现起来就是加上个判断语句
关键模拟退火算法的全局收敛性条件运用马尔科夫链的原理分析比较复杂

[1]

禁忌算法：处理TSP问题的python代码网址: https://blog.csdn.net/adkjb/article/details/81712969

[2]

模拟退火：处理TSP问题的python代码网址: https://blog.csdn.net/qq_34798326/article/details/79013338

上一篇：全力以赴优化营商环境下一篇：抖音星图短剧招商规则

同类文章推荐: 前端性能优化知识梳理; 抖音下载过的软件记录怎么查询; 拓扑结构图; 从短视频到直播，再到全域兴趣电商，2023抖音增长趋势是什么？; Steam实验室上线玩家DLC中心看看自己“省”了多少钱; 政已阅丨攻坚营商环境优化提升浙江再寻“路”

现代优化算法-启发式介绍+禁忌算法+模拟退火

咨询登记