多目标优化需要同时优化两个或者两个以上的目标函数，且不能显式地平衡它们（不存在同时优化每个目标函数的解）。

为了引出多目标优化的定义，先介绍一个概念，一个可容纳所有可行解的解子空间叫可行解空间。下面是多目标优化的定义：

给定可行解空间 和 个目标函数 多目标优化的目的是找到解 满足 是解 的目标向量。

说明：这些目标函数通常是相互矛盾的--优化其中一个目标函数会“损害”其他目标函数--因此，不可能找到对所有的目标函数都是最优解的解。所以，多目标优化的解是一组解，其中的每个解相对其他解都有其独特的优势。这种优势可以通过一些标准来衡量，一个常用的方法是帕累托最优（Pareto optimality）。

在给出帕累托最优具体定义之前先陈述一下wiki上对帕累托最优的理解：帕累托最优是指资源分配的一种理想状态。给定固有的一群人和可分配的资源，如果从一种分配状态到另一种状态的变化中，在没有使任何人情况变坏的前提下，使得至少一个人变得更好，这就是帕累托改善。帕累托最优的状态就是不可能再有更多的帕累托改善的状态。

帕累托最优是通过“占优战略”（dominant strategy）来定义的，首先定义一下“占优战略”:

给定可行解空间 和目标空间 ,是目标向量。对于两组解 :

1) 相对于 弱占优(或者说 弱劣于 )，记作 ，如果

2) 相对于 占优，记作 (或者说 劣于 )，如果

下面给出帕累托最优的定义：

给定可行解空间 和目标空间 ,是目标向量。 是帕累托最优若不存在 。帕累托最优解的目标向量的集合称为Pareto front（或者Pareto boundary）。

下图比较容易理解：

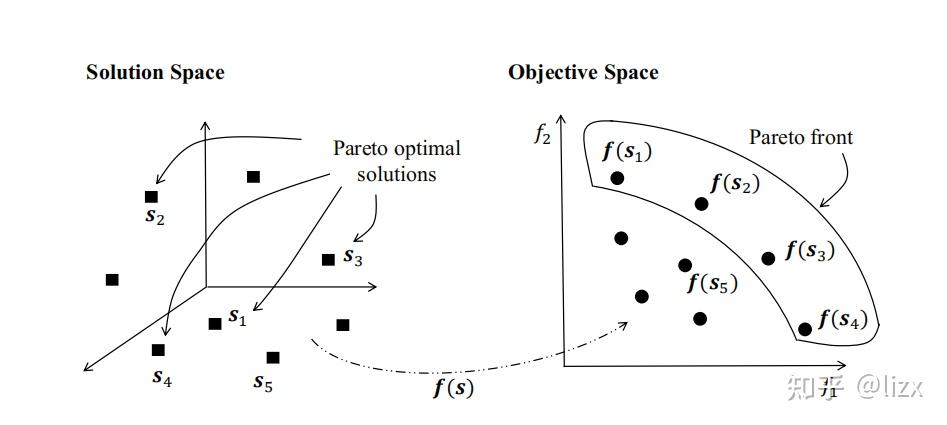
图中黑色的方块和圆点分别代表解和目标向量。可行解空间有8组解。很明显 因为 , .在这8组解中， 是帕累托最优解。目标向量 组成 Pareto front.

如果没有额外的主观偏好信息，所有帕累托最优解都被认为是同样好的。

因此，多目标优化的目标是最终目标是找到Pareto front.但是对于许多问题，找到Pareto front 是不可能的。因此，多目标优化的一种实用方法是找到一组尽可能代表帕累托最优的解。

参考文献：1. Evolutionary Learning: Advances in Theories and Algorithms. Zhi-Hua Zhou 等

2. Multi-objective optimization using genetic algorithms: A tutorial

3. 博弈论与信息经济学.张维迎

4. 帕累托最优

5.wiki